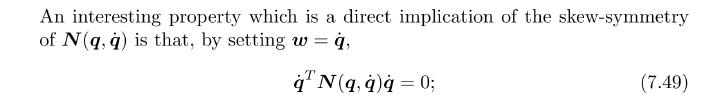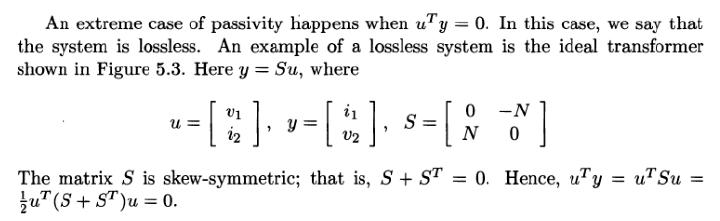Quadratic Form of a Skew Symmetric Matrix

Iacopo Moles

While reading some control theory books or papers you may stumble onto expressions like the following:

S S is a skew-symmetric matrix (i.e. S=−ST S = -S^T ) so we have XTSX=0  ∀X X^T S X = 0 \space \space \forall X

With no demonstrations whatsoever.

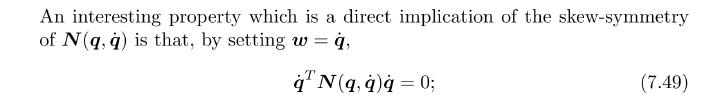
From the book: “Robotics: Modelling, Planning and Control”, Bruno Siciliano
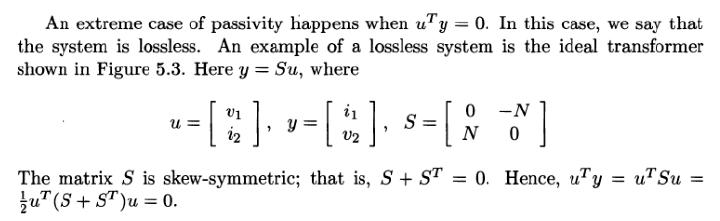
From the book: “Nonlinear Control”, Hassan K. Khalil

Let’s demonstrate it once and for all.

Proof

XTSX=n X^T S X = n

With n n a scalar. Being a scalar we have: n=nT. n = n^T.

n=nT n = n^T XTSX=(XTSX)T X^T S X = ( X^T S X)^T XTSX=XTST(XT)T X^T S X = X^T S^T (X^T )^T XTSX=XTSTX X^T S X = X^T S^T X XTSX=−XTSX X^T S X = - X^T S X n=−n  ⟺  n=0 n = - n \iff n = 0

2D Check

S=[0s−s0],X=[xy] S = \begin{bmatrix} 0 & s \\ -s & 0 \end{bmatrix}, X = \begin{bmatrix} x \\ y \end{bmatrix} XTSX=[xy][0s−s0][xy]=[xy][sy−sx]=sxy−sxy=0 X^T S X = \begin{bmatrix} x & y \end{bmatrix} \begin{bmatrix} 0 & s \\ -s & 0 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} x & y \end{bmatrix} \begin{bmatrix} sy \\ -sx \end{bmatrix} = sxy -sxy = 0
Tags: